| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Depthwise Separable Convolution
- 데이터모델링
- resnet
- pytorch
- SQL
- 엔터티
- mobilenet
- numpy
- 인접행렬
- bottleneck
- Two Pointer
- 1x1 Convolution
- SQLD
- BFS
- 연산량 감소
- 백준
- 그래프
- 인접리스트
- 정규화
- 식별자
- dp
- CROSS JOIN
- depthwise convolution
- SQLD 후기
- Inductive Bias
- skip connection
- dfs
- get_dummies()
- feature map
- outer join
- Today
- Total
SJ_Koding
백준 11053: 가장 긴 증가하는 부분수열 (실버 II) - DP 본문
11053번: 가장 긴 증가하는 부분 수열
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이
www.acmicpc.net
DP를 입문하는 문제로 피보나치수열과 부분 수열을 구하는 문제가 대표적인 것 같다. 멘토링을 하면서 DP에 조금 더 관심이 생겼는데, 정말 어려운 개념이어서 이해하는데 시간이 걸렸다. 이해를 정립시키기 위해 해당 문제를 블로그에 다시 정리하겠다.
문제요약
문제는 간단하다. 수열이 주어지면 가장 긴 부분 수열을 찾는 문제. (수열 크기 최대 1000)
ex1) [1, 100, 2, 300, 3, 4, 5] --> [1, 2, 3, 4, 5] --> 정답: 5
ex2) [10, 2, 3, 20, 30, 4, 40, 50] --> [10, 20, 30, 40, 50] --> 정답 : 5
멘토링 때 실버 II라고 해서 만만히 봤다가, DP개념 연습을 제대로 하지 않았던 나에게 바로 솔루션이 떠오르지 않았었다.
솔루션
수열 크기가 1000이기 때문에 O(N^2)으로 가능하다. 여기서 문제는 동일하지만 O(NlogN)으로만 풀 수 있는 문제는 골드II, V문제이고, 문제는 동일하지만 리스트 크기 제한이 다르다. 여기서는 1000으로 주어졌다.
이 문제는 DP로 풀어내야한다. 아래의 흐름대로 풀 수 있다.
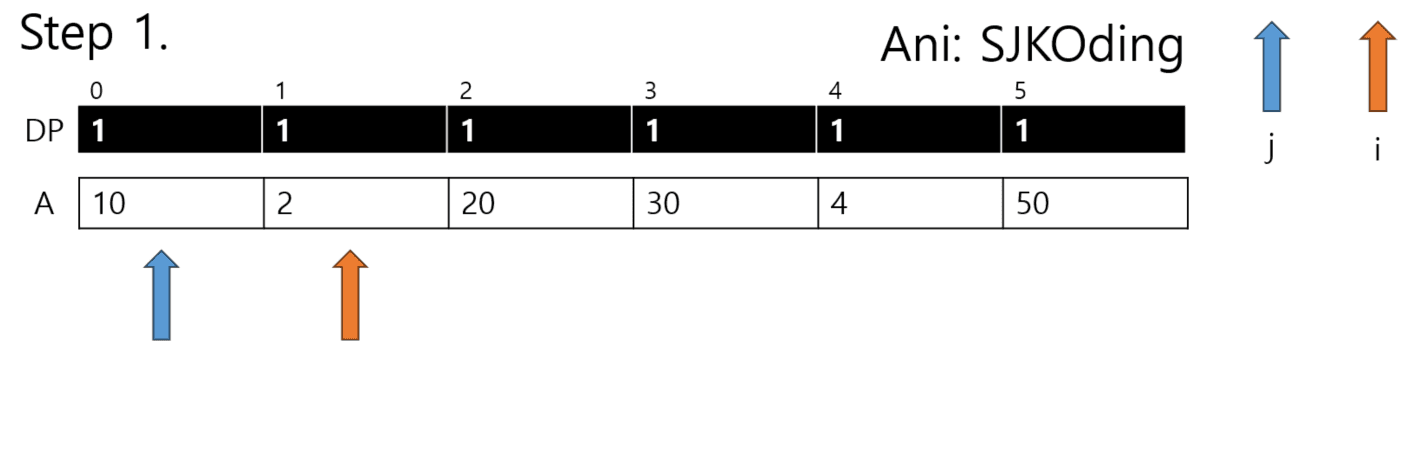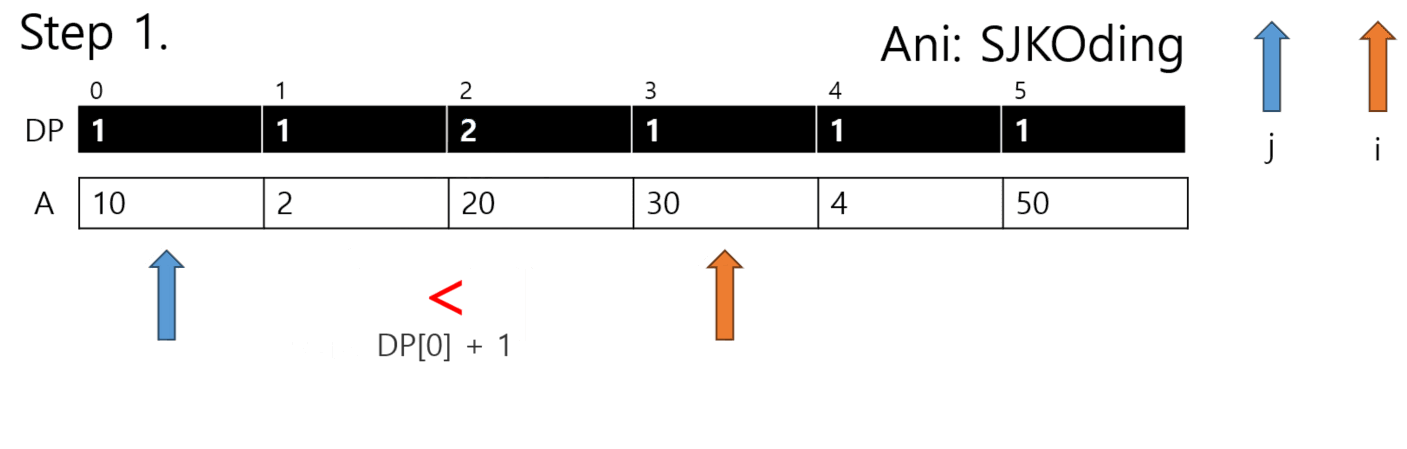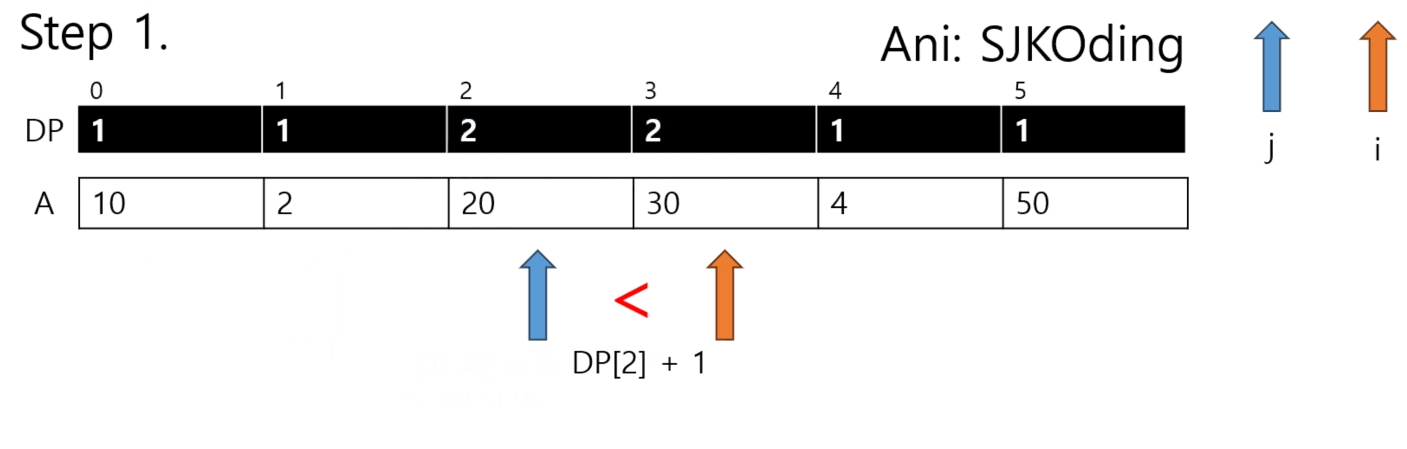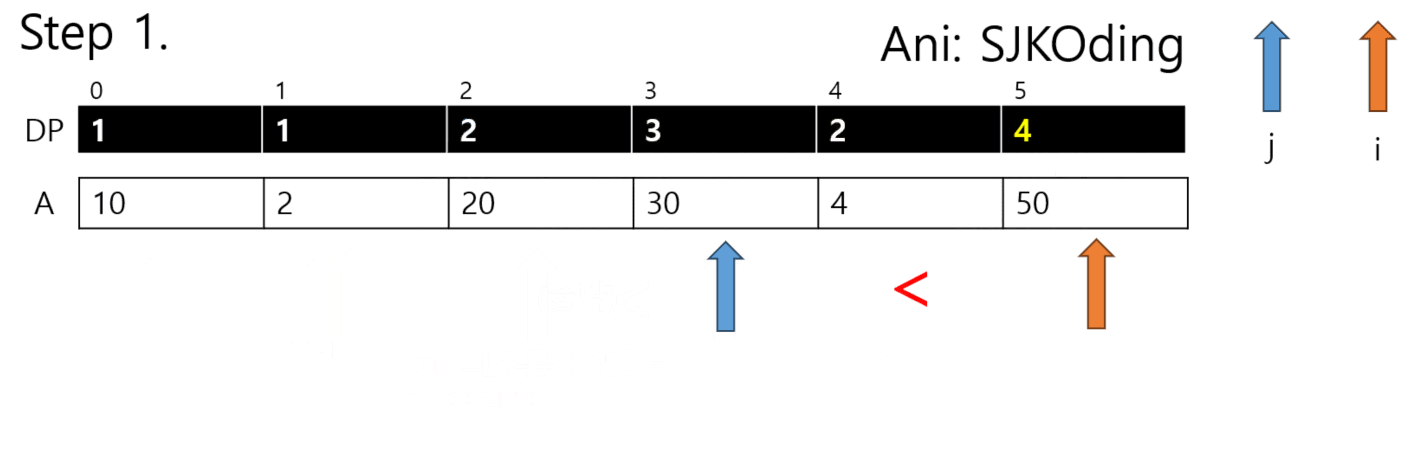
1. 단순히 수가 증가할 때 마다 카운트를 하면 위 ex1번 같은 경우, [1, 100, 300]이 기록되어 오답이 된다. 다른 방법을 이용해야한다. 그리고 모든 수를 기준으로 증가가 연속으로 얼만큼 됐는지 기록해야한다 --> DP
2. 현재 포인터를 i라고 할때, i 이전의 수 들 중 i번째 값보다 작은 j번째 값(A[j])을 찾는다.
3. dp = [1]*N 으로 선언된 리스트에서 dp[i]가 dp[j+1]보다 작다면 dp[i]를 dp[j]+1로 치환한다.
--> 이때 dp[i]가 dp[j]+1보다 작아야 한다. 그렇지 않으면 무시한다.
4. 아래 애니메이션대로 DP가 진행된다.
소스코드:
import sys
input = sys.stdin.readline
N = int(input())
A = list(map(int, input().split()))
max_cnt = 0
dp = [0] * (N+1)
for i in range(1, N):
for j in range(0, i):
if A[i] > A[j]:
if dp[i] <= dp[j]:
dp[i] = dp[j] + 1
print(max(dp)+1)
'Algorithm > DP(Dynamic Programming)' 카테고리의 다른 글
| 백준 9251: LCS (골드 IV) - DP (2) | 2024.02.28 |
|---|---|
| 백준 14002: 가장 긴 증가하는 부분수열4 (골드 IV) - DP (1) | 2024.02.27 |


