| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- SQLD
- 인접행렬
- resnet
- SQL
- Two Pointer
- dp
- Depthwise Separable Convolution
- 그래프
- pytorch
- outer join
- bottleneck
- dfs
- 식별자
- 인접리스트
- 데이터모델링
- 1x1 Convolution
- skip connection
- depthwise convolution
- feature map
- get_dummies()
- SQLD 후기
- 정규화
- 백준
- BFS
- 연산량 감소
- numpy
- CROSS JOIN
- 엔터티
- Inductive Bias
- mobilenet
- Today
- Total
SJ_Koding
manifold와 Inverted Bottleneck의 설명 본문
- 부제: ConvNeXt이해하기 5편-
(본 포스팅은 https://gaussian37.github.io 김진솔 연구원님의 MobileNet V2 블로그 글을 적극 참고하였습니다.)
일반적인 Bottleneck구조는 아래 포스팅에서 다뤘다.
Bottleneck 구조(resnet)의 설명 및 Pytorch 예시
부제: - ConvNeXt 이해하기 2편 - Bottleneck이란 용어 자체는 병목현상을 의미한다. 정말 많은 분야에서 쓰이는 말이다. 시스템 분야에서의 병목현상은 다음과 같이 정의된다. - 시스템 내에서 전체적
sjkoding.tistory.com
Manifold
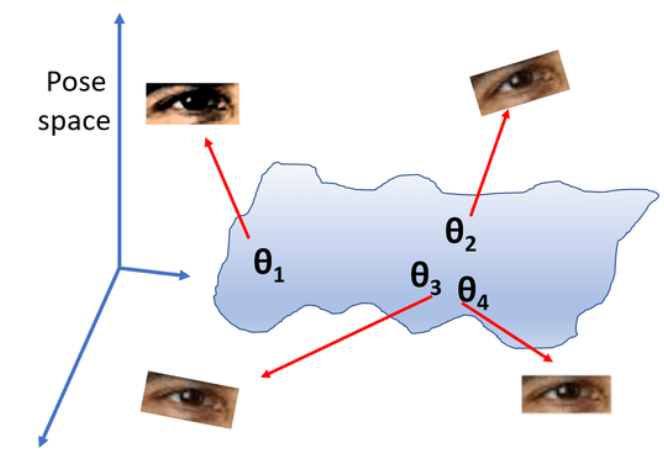
CNN에서 manifold개념은 데이터가 존재하는 고차원 공간 내에서의 저차원적 '구조'를 의미한다. CNN을 포함한 딥러닝 모델들은 고차원 데이터(이미지, 비디오 등)를 처리할 때 이러한 매니폴드(저차원적 구조)를 학습하고 탐색하려고 시도한다.
CNN은 이미지 내의 지역적인 패턴과 구조를 학습하여 저차원 manifold를 탐색하고, Conv layer와 pooling layer를 통해 점차적으로 중요한 특성을 저차원 공간에 매핑한다.
매니폴드 학습은 고차원 데이터를 저차원 매니폴드에 투영함으로써 데이터의 본질적인 특성을 보존하려는 시도이다. 즉, 주요 feature살리겠다는 의미이다. 결국 feature map에 보존되는 중요한 feature들은 manifold라고 볼 수 있는 것이다.
MobileNet2의 저자는 manifold가 ReLU를 통과하고 나서도 입력값이 양수로 남아있다면, 결국 identity matrix(0과 1로 이루어진 단위행렬)와 곱해진 단순한 선형변환(linear trasnformation)과 같다고 볼 수 있다고 한다. 따라서, ReLU를 사용하지 않고 linear transformation 역할을 하는 linear bottleneck layer를 만들어서 차원은 줄이면서 주요정보는 유지하자는 컨셉이다. 그리고 여기서 Inverted bottleneck구조가 사용되었고 이때부터 유명해지고 널리 사용되었다.
Inverted bottleneck

일반적인 bottleneck구조와 정반대로 구성되어있다. 차원을 늘린 후 피처추출을하고 다시 줄여 skip connection을 진행하는 구조이다. 저자는 저차원의 layer에 주요 정보가 압축되어있다고 가정한 후 이를 skip connection으로 사용함으로써 메모리 사용량을 줄이기 위해 위 구조를 사용한다. 또한 채널을 확장하고 standard convolution이 아닌 depthwise convolution을 사용하여 연산량을 줄였다.
*depthwise convolution은 아래의 포스팅 참고
Depthwise (Separable) Convolution의 설명 및 Pytorch 예시
- 부제: ConvNeXt이해하기 3편 - Xception에서 제시된 컨셉으로 유명해졌다. 쉽게 이해할 수 있다. 먼저 Depthwise convolution을 알기 전에 일반적인 Convolution 연산을 알아보자. 기본적인 개념으로 Input channel
sjkoding.tistory.com
정리하면 주요피처가 담긴 저차원의 feature map을 확장시켜 넓은범위에서 주요 피처를 다시 파악하고 기존 저차원에 담긴 주요 feature map과 skip connection을 진행하면서 효율적으로 더욱 많은 feature를 학습하기 위함이다.
Q: 차원을 늘려서 계산을 하는데 왠 연산량 감소?
A: 연산량을 '효율적' 으로 사용하여 더 많은 피처를 학습한다는 것에 중점을 둬야한다.
Inverted bottleneck

Inverted bottleneck 연산량
IC : Input Channel
t = expansion ratio (차원 얼마나 늘릴건지)
H: Height of feature map
W: Width of feature map
K : Kernel size
Step1: 1x1 convolution을 사용하여 t배의 채널로 확장
IC * (t * IC) * H * W
Step2: 확장된 feature map에서 KxK convolution 수행
(t*IC) * H * W * K^2
Step3: 다시 1x1convolution을 사용하여 채널 축소 (기존 IC로)
(t*IC) * IC * H * W
즉 3개를 모두 더하면 --> (t * IC) * H * W (2IC + K^2) 가 된다.
'Deep Learning' 카테고리의 다른 글
| 제3회 ETRI 휴먼이해 인공지능 논문경진대회 대상 리뷰 (ICTC2024 발표) (2) | 2024.08.12 |
|---|---|
| ConvNeXt (A ConvNet for the 2020s, facebook) 논문 리뷰 (0) | 2024.04.04 |
| Grouped convolution의 설명 및 PyTorch 예시 (1) | 2024.04.03 |
| Depthwise (Separable) Convolution의 설명 및 Pytorch 예시 (0) | 2024.04.03 |
| Bottleneck 구조(resnet)의 설명 및 Pytorch 예시 (0) | 2024.04.03 |




